15 - March - 2017 Trajectories

James Okamura
Daniel Guzman
Alejendro Rodriguez

3/15/17

In this lab,  we want to use our knowledge of projectile motion, to predict the impact point of the ball on the board.

First, we set up the apparatus as shown in the picture below.

Next, we roll a ball down the ramp and we mark where we think the ball land on the ground with tape. After that, we put a piece of paper on top of the tape mark. after that we put a carbon paper on the paper. Then we let the ball roll down the ramp and the impact would cause the carbon paper to make a mark on the paper underneath. We rolled the ball another 4 times, so a total of five marks on the paper and took the average of those distances from the table.  Also we measured the height of the table. With all that information, we can derive a formula and calculate our uncertainty. Look at the picture below.

After that we use these two formulas to help us derive an equation to help us calculate the how far down the board it will hit and its uncertainty.

In this lab, I learned that with my knowledge of projectile motion and propagated uncertainty, I can predict where a ball will have an impact on an incline board.9

13 - March - 2017 Modeling the fall of an object falling with air resistance

James Okamura
Daniel Guzman
Alejandro Rodriguez

March 13, 2017

In this lab, we are trying to figure out the relationship of force of air resistance force and the speed at which the object.

We start off this lab by going to the Design Technology building, where someone will drop the coffee filters from the balcony from 1 filter until 6 filter.

Every time the person at the balcony drop a filter, we use the video capture function on the Logger Pro Program and record the coffee filter falling. We then measured the distance where it traveled which in this case was two distances, one from top of the balcony to the very bottom of the balcony, and then the distance from the balcony to the ground.

We use these as reference scale and set it so on the Logger Pro, and later mark where the coffee filter goes every 3 frames and from that we can get our force and our velocity. By doing a linear fit on the graph, we can determine our terminal velocity for the coffee filter and we can calculate the force of the air resistance by multiply the number of coffee filter used with the mass of the coffee and the force of gravity.

After doing the above steps until you have at least 5 terminal velocity and respective force and data points we can do a power fit on the graph, to determine our k and n values. Also we ave uncertainty in our k and n values ( k is A and n is B in the table below) and our y-axis is our force of air resistance and our x-axis is our velocity of the coffee filter

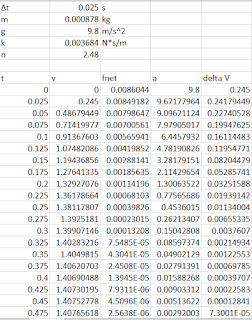
For this part of the lab, we filled out out tables with given values such as n and k values, gravity, mass and change in time. After that we were able to put in formulas in the cells to calculate time, velocity, acceleration and change in velocity. From there we look at where the velocity is close to the velocity we found in Part 1 and record those values.

And do this for each of the respective number of filters. 

We later on calculate our percent error by using the percent error formula in the picture above and with our known values for experimental velocity and the true velocity. 

I believe our model worked well on getting our velocity values since we were able to get a low percent error of 2%. I believe it may not have worked as we would have liked because there uncertainties not only in the mass but in our k and n values as well. These values will affect our velocity as a result.

8 - March - 2017 Non-Constant Acceleration Problem

James Okamura
Daniel Guzman
Alejandro Rodriguez
March 8, 2017

Objective:
In this lab, we were trying to determine the distance the object goes before coming to rest in respect to non-constant acceleration.

The initial mass is the mass of the elephant and the rocket on the elephant's back which is 6500 kg.

The initial velocity represents what velocity the elephant started with which is 25 m/s.

The burn rate is how fast the fuel burn in respect to time which is 20 kg/s.

The force represents the thrust that the rocket goes against which is opposite to the elephant's motion which is -8000 N.

The Delta T (change in time) represents the time in which everything take place in intervals of 0.10 s.

The acceleration is the deceleration the elephant has to experience so that the elephant can stop its motion with the help of the rocket, before going over the cliff, it is represented by the equation above.

There are two ways to solve this problem, the first way is to take the integral of the acceleration equation. 

Another way in solving this problem is by using Excel Spreadsheets. 

The first table is with respect to the change in time to be 0.1 second and the second table is with respect to change in time to be 0.05 seconds. When doing this method we would find the area under the slope which is delta V, and when time is small enough, it will not change. This let us know that the elephants is gradually slowing down and coming to rest which will help us determine his position from the origin which is 2.48 m.

In this lab I learned that, there are two ways in doing any calculations in lab. One way is to do it the analytical way which would involve taking the integrals and doing everything by hand. The other way is that we can use Excel Spreadsheets to make our lives by doing all the calculation for us.

6 - March - 2017 Propagated Uncertainty in measurements

James Okamura
Daniel Guzman
Alejandro Rodriguez
March 6, 2017

The object of this lab was to measure two cylindrical objects (1 Aluminum and 1 Zinc) for its height and diamter and measure those masses using a balance and with that we are able to determine the density of these two cylindrical objects.

We first obtain a caliper ( see the picture below) from the professor and was told on how to use it to measure both the diameter and height of each respective objects. We then went on to measure each masses using a balance.

The top measurements are for the Aluminum rod and the bottom measurements are for the Zinc rods respectively. When we measured each of our variable ( height, diameter and mass), we took into where the uncertainly lies within its respective measurements.

Next, we went on to calculating density of each of these two rods, but before we did that, we took the partial derivative of our density formula to help us determine our uncertainty in our density value. 

I did these calculations to determine the Aluminum rod's density with the uncertainty that lies with it.

I did these calculations to determine the Zinc's rod density with the uncertainty value that lies with it.

I believe one error we may have had when doing this lab was when we were using the caliper to measure the diameter and the height of the rods. We could have made a rounding error when we measured it so that will affect our values for density with its propagated uncertainty.

I believe one thing I learned in this lab apart from learning how to use a caliper, is how to determine the uncertainty value in our density value when our measurements we took has uncertainty in them. Uncertainty values are important because we can not truly take the exact measurement of any object, so the uncertainty value helps be relatively close to our true value. 

1-March-2017 Free Fall Lab

James Okamura
Daniel Guzman
Alejndro Rodriguez

In this lab, we are trying to  see if an object will accelerate at 9.8 m/s^2 when there are no external forces besides gravity.

This sturdy column provides a long 1.5m falling distance for an accurate reading. When the free falling body, held at the top by electromagnet, is released, its fall is precisely recorded by a spark generator on piece of spark-sensitive tape. We do this by turning the spark generator to 60 Hz causing the electromagnet to turn off and the object falling.  We then can then find the position of the free falling body by getting the tape and measuring the distance from the origin (or the first tick mark). With this information, we can plot it by velocity vs. time graph and a position vs time graph and thus help us determine the acceleration of the object.

In this lab, we decided to take the first 12 measurements of the position of the free falling object. We are able to determine that the object fell over the course 1 second ( or 60 Hz) because it would leave a mark on the spark-sensitive tape at every 1/60 second (1Hz). We were able to get the position by measuring the distance with a meter stick ( on the centimeter side) from the origin (the first mark on the tape). We got the the change in position value by subtracting the intial value from the final value each time. We are able to get the mid-interval time by dividing the time interval (1/60 s) by 2 and adding  that to our initial time value. We were able to find the V interval speed by getting our change in position value and diving that by our time frame of 1/60 second. 

This is our position vs. time graph with our change in position value on the y-axis and our mid-interval time on the x-axis. We were able to get the formula of this graph by doing a liner fit on the graph and by displaying the equation and R^2 value.

This is our velocity vs. time graph in which we were able to get with our V interval speed values on the y-axis and our mid-interval time values on the x-axis. We were able to get the formula by first doing a linear fit of the graph and by then displaying the equation and the R^2 value.

Questions/Analysis

1.When you solve for acceleration, you can solve it in two ways, first you get the average velocity and divide that by that time interval, and the second way is to get the velocity at the mid point ( which is the same as the average velocity given the time interval is the same ) and divide that by that time frame.

2. You can get the the acceleration due to gravity from the velocity vs. time graph by taking the 1st derivative of the equation of the graph. Our value is way off as our value is 960 cm/s^2 compared to accepted value of gravity which is 980 cm/s^2.

3. You can get the acceleration due to gravity from the position vs. time graph by taking the 2nd derivative of the equation of the graph. When you take the 2nd derivative of the equation, you get a value of 957.48 cm/s^2 which is off because our accepted value of gravity is still 980 cm/s^2.

The patterns that I see makes sense because the position and velocity would increase with respect to time due to gravity. I believe the reason why we were off and made values have some uncertainty is because when the object fell, we did not take into account friction of the tape on the object and air resistance that acts against the object as it falls. 

The percent difference we got is 2.04 %. This value represents how far away we were from the accepted value.

The second column values are the values that our classmate had gotten for their experimental value for gravity in cm/s^2. Afterwards we got the mean of those experimental values by adding all 10 values and dividing by 10, which is located in the 5th column, We were able to get the deviation value by subtracting the mean of gravity value from the experimental values found at each table. We were able to get the deviation^2 value by squaring all the deviation values we found previously. We go the average deviation^2 by taking the average of all deviation ^2 values. We got the standard deviation value by taking the standard deviation of the deviation values on our spreadsheet.

Questions/ Analysis

1. The patterns I found in our value of g is that they were all relatively close to 960 cm/s^2 but still far away from the accepted value of 980 cm/s^2.

2.Our average value of g, which is 961.156 cm/s^2 compared to the accepted value of g, is that we are still far away.

3. The pattern we found in the class' values of g is that there are far from the accepted value of g when we look at it by the standard deviation values.

4. The systematic errors are that of air resistance against the object as it fall in free fall and the friction between the free fall object and the tape, when it is marking the tape. Our random error is that when we measured the position of the object, distance, we might have not gotten the exact value for the position and may have rounded.

5. I believe the key point of this lab apart from knowing how to measure a free falling object with the given apparatus, is that to understand how to look derive an acceleration from the velocity vs. time graph and position vs. time graphs. Another point was to know how far (or close) we were from the accepted value for gravity. With this lab, I learned how to apply statistics aspects to it and learn more on how to use Excel spreadsheets for lab.

27-Feb-2017: Mass and Period from an Internal Balance

James Okamura

Daniel Guzman 

Rodrigo

Frebruary 27, 2017

In this lab we were trying to measure masses of known and unknown objects that doesn't depend on gravity with a Inertial Balance.

This apparatus is called an Internal Balance and we put a tape on the end with the sensor near the tape. Then when we add known masses we would record what mass we out on, and using Logger Pro, we are able to record the period of the oscillations . With this given data of known masses and respective periods we are able to calculate the measurement of the Internal Balance tray. 

This data table is where I recorded the known masses values with its respective periods when using the Internal Balance and Logger Pro.

Using Logger Pro, we were able to get natural log of the period value and the natural log of the known masses. From there we were able to calculate our upper and lower bounds as well as our middle bound by comparing the linear correlations in which we were able to obtain 350 grams and 310 grams ( max and min respectively) with each a correlation of 0.9998.

When we graph with the tray value with 310 grams and 350 grams we were able to calculate the slopes and Y-intercepts from the Logger Pro program.

Using these two formulas, we are now able to find the range of masses of an unknown object using the Internal Balance. We did this by putting an unknown object, (for our case we used a tape dispenser and a calculator ) on the Internal Balance and swung it so that the motion sensor will record its respective  period. Using the recorded periods and the the two formulas above, we are able to find the range of masses for the tape dispenser and calculator. 

I believe that when we calculated the range of mass values for calculator, there was some for of human error that took place, such as how we placed the calculator, or if interpreted the data wrong so it is not in the range as shown above. When we did the tape dispenser, we got the range to be really close to the actual measurement from a balance.

I believe in this lab , what we did was how to use an internal balance and logger pro to help us find the associatio between the mass of an object to its period.